What Does It Mean to Interpret the Slope
2.vi: Interpreting the Slope of a Line
- Folio ID
- 19635
Learning Outcomes
- Interpret the gradient of a line as the alter in \(y\) when \(x\) changes by i.
A mutual issue when we learn about the equation of a line in algebra is to land the slope as a number, but take no idea what it represents in the real world. The slope of a line is the rise over the run. If the gradient is given by an integer or decimal value we can always put it over the number one. In this instance, the line rises by the gradient when information technology runs i. "Runs 1" means that the x value increases by 1 unit. Therefore the slope represents how much the y value changes when the x value changes by 1 unit of measurement. In statistics, especially regression analysis, the x value has real life meaning and so does the y value.
Example \(\PageIndex{1}\)
A study was washed to see the relationship between the time it takes, \(x\), to complete a college degree and the pupil loan debt incurred, \(y\). The equation of the regression line was plant to be:
\[y=25142\:+14329x\]
Interpret the slope of the regression line in the context of the study.
Solution
First, note that the slope is the coefficient in front of the \(x\). Thus, the slope is 14,329. Adjacent, the slope is the ascent over the run, so it helps to write the slope as a fraction:
\[Slope\:=\frac{\:rise}{run}=\frac{14,329}{i}\]
The rising is the change in \(y\) and \(y\) represents student loan debt. Thus, the numerator represents an increase of $fourteen,329 of pupil loan debt. The run is the change in \(ten\) and \(ten\) represents the fourth dimension information technology takes to complete a college degree. Thus, the denominator represents an increment of 1 year to complete a college degree. We can put this all together and interpret the slope equally telling us that for every additional year it takes to complete a higher degree, on average the student loan debt increases past $14,329.
Example \(\PageIndex{two}\)
Suppose that a research group tested the cholesterol level of a sample of xl year old women and then waited many years to see the relationship between a woman's HDL cholesterol level in mg/dl, \(10\), and her age of death, \(y\). The equation of the regression line was plant to exist:
\[y=103\:-0.3x\]
Translate the slope of the regression line in the context of the report.
Solution
The slope of the regression line is -0.three. The slope as a fraction is:
\(Slope\:=\frac{\:rise}{run}=\frac{-0.3}{1}" width="233\)
The rise is the alter in \(y\) and \(y\) represents age of death. Since the gradient is negative, the numerator indicates a decrease in lifespan. Thus, the numerator represents a decrease in lifespan of 0.3 years. The run is the change in \(x\) and \(x\) represents the HDL cholesterol level. Thus, the denominator represents an HDL cholesterol level increase of one mg/dl. Now, put this all together and translate the slope every bit telling u.s.a. that for every additional 1 mg/dl of HDL cholesterol, on average women are predicted to die 0.3years younger.
Example \(\PageIndex{3}\)
A researcher asked several employees who worked overtime "How many hours of overtime did yous piece of work last calendar week?" and "On a scale from 1 to 10 how satisfied are you with your task?". The scatterplot and the regression line from this study are shown beneath.
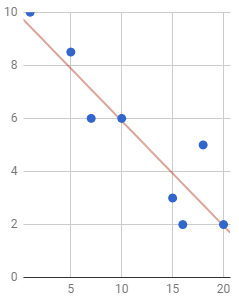
Translate the gradient of the regression line in the context of the study.
Solution
We first need to determine the slope of the regression line. To find the gradient, we become two points that accept as squeamish coordinates as possible. From the graph, we see that the line goes through the points (x,6) and (xv,4). The slope of the regression line tin can at present be found using the ascent over the run formula:
\[Slope\:=\frac{\:ascent}{run}=\frac{four-6}{fifteen-10}=\frac{-2}{5}\]
The rise is the change in \(y\) and \(y\) represents job satisfaction rating. Since the gradient is negative, the numerator indicates a subtract in job satisfaction. Thus, the numerator represents a decrease in task satisfaction of 2 on the calibration from 1 to 10. The run is the alter in \(x\) and \(x\) represents the overtime work hours. Thus, the denominator represents an increase of 5 hours of overtime work. At present, put this all together and interpret the slope every bit telling u.s.a. that for every additional five hours of overtime work that employees are asked to do, their job satisfaction goes down an boilerplate of 2 points.
Do
The scatterplot and regression line beneath are from a written report that collected data on the population (in hundred thousands) of cities and the average number of hours per week the city's residents spend outdoors.
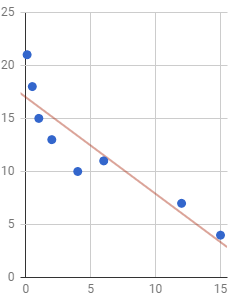
Interpret the slope of this regression line in the context of the study.
Interpret the Meaning of the Slope of a Linear Equation - Smokers
Interpreting the Slope of a Regression Line
mcclurecoursentand1937.blogspot.com
Source: https://math.libretexts.org/Courses/De_Anza_College/Pre-Statistics/2%3A_Graphing_Points_and_Lines_in_Two_Dimensions/2.6%3A_Interpreting_the_Slope_of_a_Line
0 Response to "What Does It Mean to Interpret the Slope"
Post a Comment